An Evaluation of the RSA Private Keys and the Presence of Weak Keys

Abstract

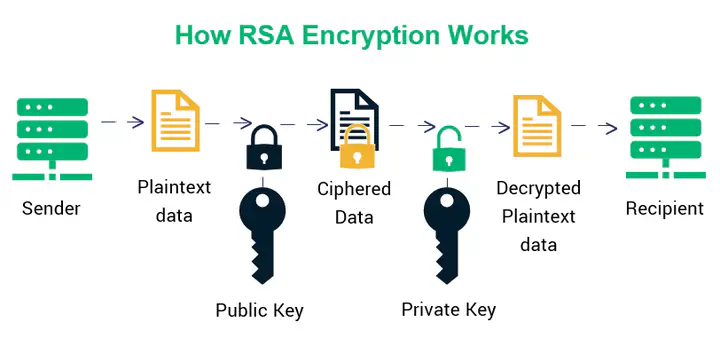
Numerous applications that rely on assymmetric cryptography use the RSA algorithm. It can be applied to digital signatures and the encryption of sensitive data. The secure storage of the private key is essential for the algorithm’s strength. Finding ways to use factorization or other heuristics to determine the value of the private key was the goal of several academic efforts. The Euler totient or the Carmichael functions are both used in this study to analyze the private key properties and demonstrate the existence of many private keys for the same public key. We further demonstrate that a universal key that complies with the FIPS standard exists. Moreover, by taking advantage of a condition imposed by FIPS recommendations, we present a new method for attacking the RSA modulus (N). The attack is based on the value of the private key being greater than 2^(n/2) with n representing the modulus size.

Zakarea Alshara

Associate Professor of Software Engineering

My research interests include Software Engineering, Software Security, AI, and Cloud Computing.